產(chǎn)品介紹?
? 航空燃?xì)廨啓C(jī)和渦輪機(jī)振動診斷的重要方向是建?模診斷。建模提供了一個(gè)機(jī)會，將某些機(jī)器缺陷的存?在與振動信號中存在的跡象聯(lián)系起來。其中一個(gè)缺陷?是航空發(fā)動機(jī)和渦輪機(jī)軸出現(xiàn)裂縫是不允許的。因?此，診斷系統(tǒng)重要的任務(wù)是及時(shí)檢測裂紋并預(yù)測其?進(jìn)展。轉(zhuǎn)子中出現(xiàn)裂紋，導(dǎo)致局部剛度降低。剛度損失?的值取決于裂紋的幾何特性。如果施加重力等靜載?荷，轉(zhuǎn)子旋轉(zhuǎn)時(shí)裂紋打開和關(guān)閉。因此，軸的剛度每?一個(gè)周期都會發(fā)生變化。轉(zhuǎn)子系統(tǒng)的裂紋導(dǎo)致振動信?號[1]發(fā)生以下變化：?·?由于剛度降低引起的靜態(tài)偏轉(zhuǎn)的增加，轉(zhuǎn)速1?倍諧波振幅增加。?·?由于轉(zhuǎn)子剛度不對稱，轉(zhuǎn)速的2倍分量的外?觀。?·?由于裂紋的周期性開閉而旋轉(zhuǎn)的3х轉(zhuǎn)速部件?的出現(xiàn)。該數(shù)學(xué)模型的主要任務(wù)是考慮盡可能多的因素，?描述裂紋發(fā)生部位剛度局部變化的值和規(guī)律。?有幾種方法可以模擬裂縫。在較簡單的情況下，?通過降低整個(gè)軸[2,3,4]的徑向剛度來模擬裂紋。在其?他情況下，發(fā)生裂縫的軸部分被等效的梁元件所取?代。計(jì)算這些元素的剛度矩陣的系數(shù)，考慮裂縫和變?化的每個(gè)周期。在工作中，利用考慮裂紋的梁截面的?慣性矩計(jì)算有裂紋的梁構(gòu)件的剛矩矩陣。在工作中，?根據(jù)固體破壞力學(xué)方程計(jì)算了該元素的[6]剛度矩陣。?可通過連接軸位置的邊界部分來模擬裂紋，并給出裂?紋力矩剛度[7,8]。?當(dāng)轉(zhuǎn)子旋轉(zhuǎn)時(shí)，根據(jù)其開關(guān)的不同而產(chǎn)生的裂紋?剛度的變化，可以用不同的數(shù)學(xué)方法來描述。在最簡?單的情況下，可以假設(shè)裂紋只有兩個(gè)位置：完全?打開或完全關(guān)閉，階躍函數(shù)可以用數(shù)學(xué)方法來描述其?剛度變化[4]。Work[3]描述了最廣泛的剛度變化模?型。其中之一是加斯奇方程。剛度的變化取決于靜力?相位和裂紋相位之間的夾角，由傅里葉級數(shù)的17次諧?波描述。同一篇文章給出了梅斯和戴維斯方程，其中?剛度隨角度根據(jù)余弦定律而變化。在楊模型中，剛度?隨余弦定律的變化?研究人員提供的深度。?本文在現(xiàn)有方法的基礎(chǔ)上建立了裂紋模型，并提?出了突出精確轉(zhuǎn)子檢測指標(biāo)的方法。?該算法包含在動力學(xué)R4軟件程序[9]中，該程序?代表了對復(fù)雜轉(zhuǎn)子系統(tǒng)動態(tài)行為計(jì)算的專用系統(tǒng)。
裂縫模型?
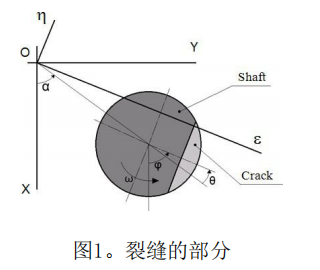
? 在公認(rèn)的模擬概念中，軸模型中的裂紋被替換為?一個(gè)彈性鏈接，將軸分為兩個(gè)部分，并用可變系數(shù)的?剛度矩陣來描述。如果無裂紋，則完成軸部件部分之?間的應(yīng)變相容性條件，因此禁止所有相互位移。我們?介紹了位于裂紋區(qū)域的旋轉(zhuǎn)坐標(biāo)系ηOε，圖1。它的?起源與固定坐標(biāo)系XYZ的起源重合。軸執(zhí)行兩個(gè)運(yùn)動，?繞Z軸適當(dāng)旋轉(zhuǎn)和進(jìn)動。當(dāng)描述裂紋時(shí)，我們只考慮圍?繞η軸和ε軸的旋轉(zhuǎn)。在其他自由度下的位移被忽略?了。
旋轉(zhuǎn)坐標(biāo)系中模擬裂紋的彈性矩陣可寫如下：
?
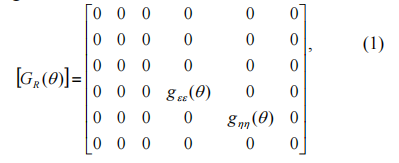
? 在哪里q = j -a相位差，jj?-軸的旋轉(zhuǎn)不同角度，α?-?進(jìn)動角；??gee?(q)和ghh?(q?) -?變量彎矩彈性系數(shù)。
? 靈活性取決于角度q因?yàn)楫?dāng)軸旋轉(zhuǎn)時(shí)，裂紋會打開和關(guān)閉。 剛度矩陣是通過對?[GR?(q)]矩陣求逆得到的，主對角線上的零柔度系數(shù)導(dǎo)致獲得趨于無窮大的剛度系數(shù)。 我們將此類剛度系數(shù)的值限制為 1е10 N/m； 這個(gè)假設(shè)對結(jié)果沒有顯著影響，即我們得到
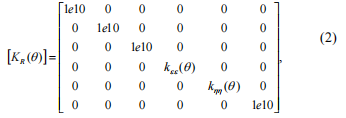
使用以下等式將剛度矩陣轉(zhuǎn)換為固定坐標(biāo)系：
在哪里[T]-旋轉(zhuǎn)矩陣（4），在哪里C1 = cos(j), S1 = sin(j).
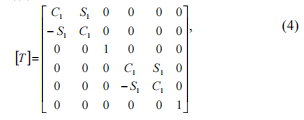
乘以與等式（3）對應(yīng)的矩陣，我們得到：
? ??我們進(jìn)行了一些轉(zhuǎn)換，使我們有機(jī)會更簡單地描述裂紋剛度矩陣及其系數(shù)獲取算法。 與 Maes 模型相對應(yīng)，可以假設(shè)有裂紋的圓梁的徑向柔度由余弦定律從最小值變?yōu)樽畲笾怠?span style="color: rgb(0, 0, 0); font-family: " times="" new="" font-size:="">
?其中 g0 - 無裂紋梁的柔度（最小值），gc - 有開裂梁的柔度（最大值）。
?我們用彎矩剛度kinit?mh???的鉸鏈代替裂紋。 梁邊界條件應(yīng)提供其靜態(tài)可定義性，如圖 2 所示。
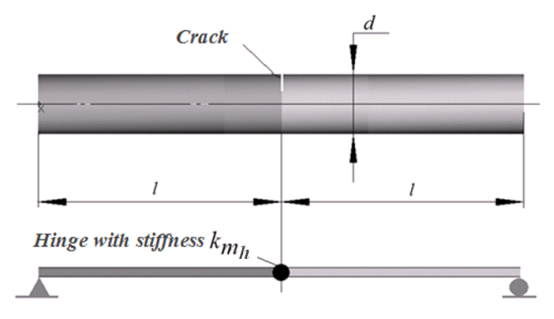
圖2 鉸鏈置換裂紋
則得到開裂軸突出部分的徑向撓度為：
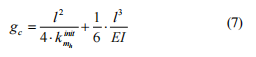
? ?其中 E - 楊氏模量，I - 軸截面的徑向慣性矩，kinit mh - 對應(yīng)于完全開放裂紋的等效連桿的力矩剛度系數(shù)。
? ??該方程有兩個(gè)被加數(shù)——與裂紋有關(guān)的柔度和無裂紋梁的柔度。 它需要注意的是，無論梁的形狀、邊界條件和裂紋位置如何，其對一般梁柔韌性的貢獻(xiàn)僅取決于系數(shù) kinit mh ，即 第一個(gè)求和。
? ?當(dāng)梁旋轉(zhuǎn)時(shí)，裂紋截面的柔韌性會發(fā)生變化。 我們得到以下信息：
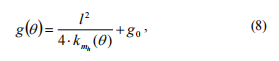
? ? 哪里?go=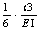
-無裂紋梁的柔韌性，(q) kmh- 給定q的當(dāng)前力矩剛度系數(shù)。
將兩個(gè)方程（5）和（7）積分，我們得到：
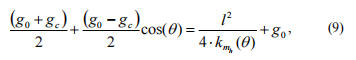
? ? 其中服用式（6）考慮我們得到變化的規(guī)律力矩剛性取決于階段?q?差異：
????
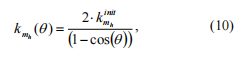? ? ?獲得的等效連桿的力矩剛度僅取決于軸直徑、材料特性和裂紋深度。 軸中裂紋位置的變化，包括支撐單元在內(nèi)的軸的特性不會改變等效連桿的力矩剛度（在
條件是有裂紋的截面在有裂紋的截面的任何部分保持不變
獲得）。
? ?回到之前得到的剛度矩陣，其剛度系數(shù)可寫為：
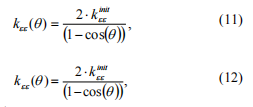
其中?k?initee?, kinithh??-全開裂紋對應(yīng)軸上的力矩剛度初始值。
?kinitee??, kinithh?計(jì)算的任務(wù)可以通過兩種方式解決。 第一個(gè)是矩的計(jì)算FEM 程序中的剛度。 二是運(yùn)用斷裂力學(xué)理論。 如果已知開裂的幾何形狀、軸直徑和材料特性 [7,10]，則可以計(jì)算開裂局部撓度系數(shù)的值。
? ?帶裂紋轉(zhuǎn)子系統(tǒng)的仿真算法
? ?應(yīng)通過以下步驟來獲得裂紋的力矩剛度系數(shù)。
1. 完整的轉(zhuǎn)子模型是在專門的程序之一中創(chuàng)建的，用于分析轉(zhuǎn)子動力學(xué)（對于例如，在 Dynamics R4 中）。
2. 有裂紋的轉(zhuǎn)子部分高亮顯示。
3. 裂縫將軸段分成兩個(gè)子系統(tǒng)。 由變量矩陣描述的鏈接
剛度系數(shù)?[K(q,j)]的尺寸為 6x6 放置在子系統(tǒng)之間。
4. 開裂的初始力矩剛度系數(shù)kinitee ?, kinithh?由給出的方法得到多于。 這些數(shù)據(jù)是用于計(jì)算的初始數(shù)據(jù)。
結(jié)合運(yùn)動方程計(jì)算連桿模擬裂紋剛度矩陣系數(shù)
每個(gè)q的轉(zhuǎn)子系統(tǒng)。 在描述非線性動力模型的非線性陳述矩陣方程轉(zhuǎn)子系統(tǒng)如下：
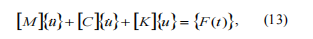
? ? ? ?其中[M ] – 慣性系數(shù)矩陣;?[C] – 阻尼和陀螺儀系數(shù)矩陣 [K] - 剛度系數(shù)矩陣; { u&&}?,{ u&}?,{u} – 相應(yīng)的振動加速度、振動速度和振動位移列; {F(t)} - 任何類型的動態(tài)載荷——內(nèi)部和外部。
等效連桿的剛度矩陣可分為常量和變量兩部分，下列為真：
? ?[KC ] 包含在 [K] 系統(tǒng)的一般剛度矩陣中。 矩陣 ( ) [ q j ] n , K 用于計(jì)算非線性連接的反應(yīng)：
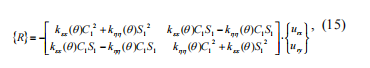? ? ?其中urx?, ury– 截面圍繞相應(yīng)軸的相互旋轉(zhuǎn)。系統(tǒng)的最終運(yùn)動方程為：
? ?
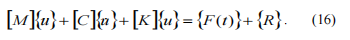
?給定的方程可以用數(shù)值方法求解，如 Runge-Kutta 法、Newmark 法等。
? ? 建議算法的充分性是通過比較兩個(gè)支撐梁的靈活性與
在有限元系統(tǒng)中并根據(jù) Dynamics R4 中的假定算法獲得的裂紋。 任務(wù)是計(jì)算裂紋和力之間不同階段的裂紋截面中單位力作用下的梁撓度。
? ? 圖 3 顯示了建議算法的檢查結(jié)果。 比較三個(gè)結(jié)果：
- 使用有限元法 (FEM) 計(jì)算柔韌性。 在有限元系統(tǒng)中計(jì)算了裂紋梁模型的徑向柔度，適用于裂紋角位置的整個(gè)范圍；
- 使用 Dynamics R4 計(jì)算靈活性，使用 FEM 獲得初始數(shù)據(jù)。?
? ? 全開裂紋的力矩剛度初始值?kinitee?,?kinithh是求解方程（7）的kinitmh得到的，并用有限元法計(jì)算相應(yīng)方向有裂紋 gc 的梁的徑向柔度。 根據(jù)（10）定律，中間角裂紋位置的彎矩剛度從較小值變?yōu)檩^大值；
? ?- 使用 Dynamics R4 計(jì)算靈活性。 完全開放裂紋的彎矩初始數(shù)據(jù)?kinitee??,?kinithh??使用斷裂力學(xué)算法[7, 10] 解析獲得。 力矩靈活性值中間角裂紋位置根據(jù)定律 (10) 從較小值變?yōu)檩^大值。
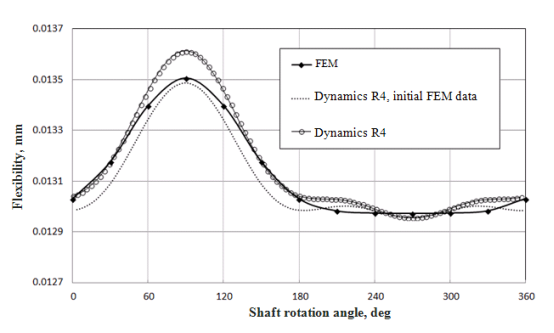
圖 3 每轉(zhuǎn)一圈裂紋截面梁柔度的變化
? ? ?
??FEM 模型的計(jì)算結(jié)果與 Dynamics R4 中的模型計(jì)算結(jié)果相近。 通過分析獲得的初始條件的計(jì)算結(jié)果與 FEM 結(jié)果的差異小于 1%。 同時(shí)，初始剛度的分析計(jì)算速度比 FEM 計(jì)算快得多，并且需要更少的工作時(shí)間，因此更易于使用。
有裂紋轉(zhuǎn)子的幾何形狀和參數(shù)
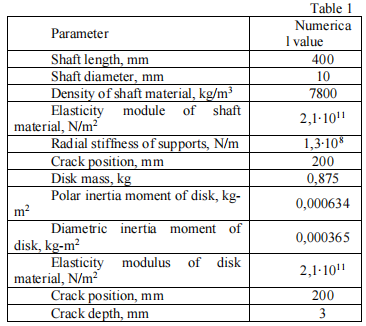
? ?選擇帶裂紋轉(zhuǎn)子的幾何形狀以顯示算法工作的最佳優(yōu)勢，如表 1。帶有中心盤的轉(zhuǎn)子，支架放置在軸端。
仿真結(jié)果
為了顯示裂紋對動態(tài)轉(zhuǎn)子行為的影響，轉(zhuǎn)子加速度在 0 到
4000 轉(zhuǎn)。 只有重力有外部影響。 這種轉(zhuǎn)子的第一個(gè)臨界速度為wcr?=2643,6 rpm (44,06 Hz)。 圖 4 顯示了獲得的幅頻特性。
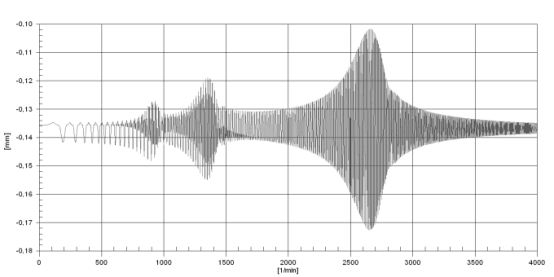
圖 4 裂紋截面的幅頻特性
? ? 在距臨界速度 1/3 和 1/2 處，參數(shù)共振是力矩循環(huán)變化的結(jié)果出現(xiàn)僵硬。 級聯(lián)圖顯示了 1x、2x 和 3x 轉(zhuǎn)子諧波，圖 5。
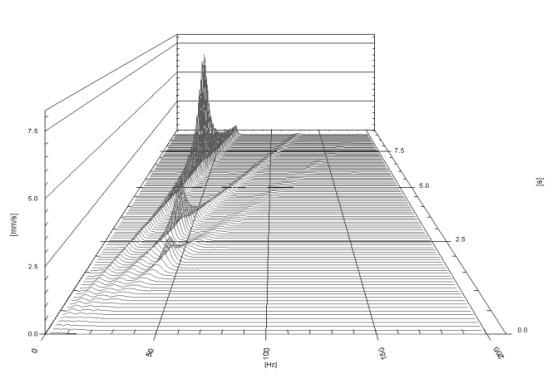
圖 5 轉(zhuǎn)子加速至 4000 rpm 時(shí)的振動速度級聯(lián)圖
下面給出了動態(tài)轉(zhuǎn)子特性（光譜和軌道）在w =1/3wcr?, w =1/ 2wcr ,w = wcr?。 只有轉(zhuǎn)子重量代表外部載荷。
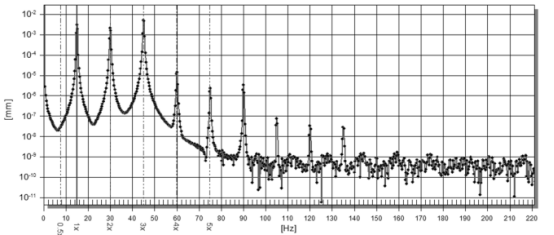
圖 6 對數(shù)坐標(biāo)中1/3 wcr區(qū)域的信號頻譜
圖 7 線性坐標(biāo)中1/3 wcr?區(qū)域的信號譜
圖 81/3 wcr狀態(tài)下裂紋截面轉(zhuǎn)子中心軌道
圖 9 對數(shù)坐標(biāo)中1/2 wcr區(qū)域的信號譜
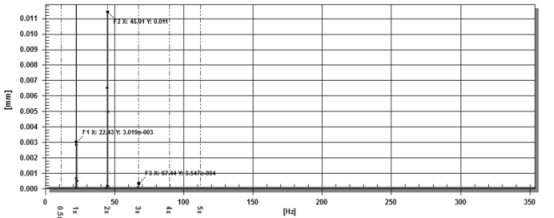
圖 10 線性坐標(biāo)中1/2 wcr?區(qū)域的信號頻譜
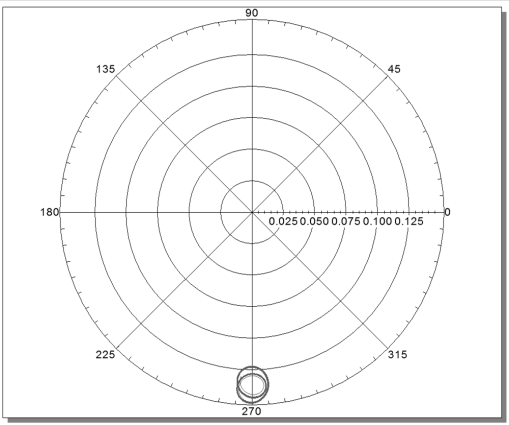
圖 11?1/2 wcr?狀態(tài)下裂紋截面轉(zhuǎn)子中心軌道
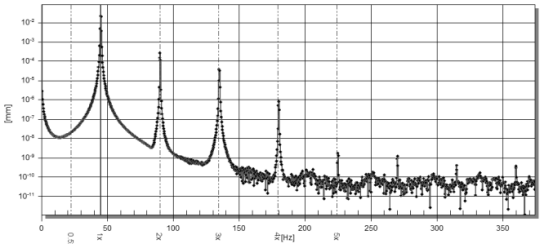
圖 12wcr?區(qū)域的對數(shù)坐標(biāo)信號譜
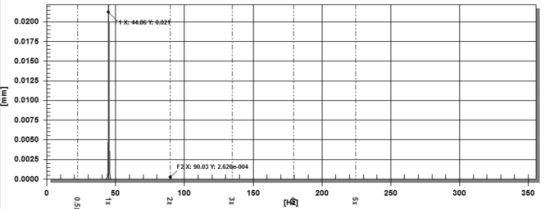
圖 13 線性坐標(biāo)中wcr區(qū)域的信號譜
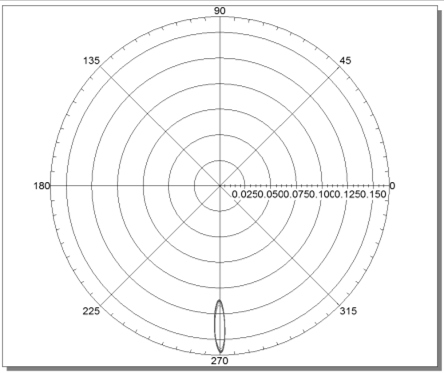圖 14wcr?狀態(tài)下裂紋截面轉(zhuǎn)子中心軌道
? ?
? 獲得的結(jié)果表明，次諧波共振的出現(xiàn)可能是裂紋出現(xiàn)的診斷標(biāo)志。 檢測多個(gè)轉(zhuǎn)子諧波的最佳診斷機(jī)制是第一臨界速度的 1/3 范圍。 轉(zhuǎn)子頻率的三個(gè)諧波幅值接近于它。
? ? 結(jié)論
? ? 開發(fā)的裂紋模型在帶裂紋轉(zhuǎn)子動態(tài)特性分析算法中的應(yīng)用
大大減少了建模和分析所需的時(shí)間。計(jì)算結(jié)果表明，軸的裂紋所研究的轉(zhuǎn)子在1/3?wcr?, 1/3?wcr?,?wcr?狀態(tài)下引起參數(shù)共振，這是轉(zhuǎn)子的結(jié)果頻率為 1x、2x、3x、4x 等的諧波。在實(shí)際測試中，有機(jī)會突出顯示兩個(gè)或三個(gè)轉(zhuǎn)子諧波。存在次諧波共振、多次諧波和軸運(yùn)動軌道的變化斷面可能有裂紋出現(xiàn)的跡象。同時(shí)應(yīng)該考慮到的概率在實(shí)際實(shí)踐中檢測裂紋取決于其幾何形狀和深度、所用設(shè)備的靈敏度、軌道傳感器的存在等。因此，所提出的模型應(yīng)主要被視為在振動診斷領(lǐng)域培訓(xùn)工程師的工具，并獲得限制裂紋診斷標(biāo)志的值。
?